Frequency-dependent phase-shift measurement is often used to account for dispersion in surface-wave FWI. However, when multiple surface modes (fundemental + overtones) simultaneously exist in the window, it is desirable to measure the phase shift each mode separately. Due to the difference in group velocity, different modes are often separated in time. In such cases, frequency-time-dependent phase-shift measurement, using arrival time as a proxy of mode, is more appropriate.
Continuous wavelet transform (CWT) is an effective tool to extract frequency-time-dependent information of a signal. Here I provide a demonstration to perform frequency-time-dependent phase-shift measurement using CWT.
CWT of a time series $u(t)$ is defined as:
$$W[u](l,\tau) = \int_0^T w(l,t-\tau)u(t)\mathrm{d}t,$$where $w(l,t-\tau)$ is some mother wavelet rescaled by $l$, and then centered at $\tau$. The mother wavelet is designed to have a fixed number of cycles within a duration of $l$, meaning that the scale $l$ is a proxy of frequency of the signal.
CWT can be efficiently performed in Fourier domain. Derivation of the adjoint source is also trivial. In real FWI practice, it is desirable to filter the measurement according to certain criterions, potentially useful ones are (1) limiting $l$ such that the measurement focuses on frequency band of interest, (2) the magnitude of $W[u](l,\tau)$ in the data (and/or synthetics) should be significant to avoid being contaminated by noise and (3) the phase shift should be small to avoid cycle skipping.
The numerical example below involves multi-mode dispersive waveforms controled by certain parameters. Inversion is performed to adjust these control parameters to fit "synthetics" to "data". For now, the experiment is noise-free, and the robustness to noise is to be investigated. The experiment is performed with PyTorch such that all the necessary gradients are calculated with auto-differentiation.
!pip install pycwt
# install and import pycwt
from pycwt import Morlet
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from matplotlib import rc
from matplotlib.animation import FuncAnimation, PillowWriter
from IPython.display import HTML
I first implement the generation of the multi-mode dispersive wave
$$\mathrm{e}^{-\frac{(t-t_0)^2}{2\sigma_t^2}}\mathrm{cos}(2\pi(f_c+\frac{\sigma_f}{\sigma_t}(t-t_0))+\varphi_0)$$This is motivated by the vibroseis function, where the instaneous frequency increases linearly with time. $\sigma_t$ and $\sigma_f$ determine the duration of the signal and the width of the frequency band, respectively. $t_0$ and $f_c$ control centroid time and frequency. $\varphi_0$ provides a constant phase shift. The goal is to invert for these five parameters that control the shape of the waveform. In real FWI, the unknowns to be inverted are the structural parameters and are therefore much more complex. Note that the amplitude information is not reliable and cannot be used, which prohibits the use of the $L^2$ waveform misfit. This is both the case in this experiment and in real FWI practice.
class MultiModeWave(nn.Module):
def __init__(self, npts, dt, has_amplitude=False):
super(MultiModeWave, self).__init__()
self.t = nn.Parameter(torch.from_numpy(np.array(range(0, npts), dtype=float) * dt), requires_grad=False)
self.has_amplitude = has_amplitude
def forward(self, inp_par):
t0 = inp_par[0]
sigma_t = inp_par[1]
fc = inp_par[2]
sigma_f = inp_par[3]
if self.has_amplitude:
A = inp_par[5]
else:
A = 1.0
phi0 = inp_par[4]
k = sigma_f / sigma_t
f = fc + (self.t-t0) * k
return A * torch.exp(-(self.t-t0)*(self.t-t0)/2.0/sigma_t/sigma_t) * torch.cos(2.0*np.pi*f*(self.t-t0)+phi0)
Next, I implement the wavelet-based frequency-time-dependent measurement as described above. The code is largely based on the implementation of the pycwt package. For purpose of comparison, I also implement the Fourier-based frequency-dependent measurement. Note that in both cases, only phase-shift information is preserved. Measurements are filtered using the three criterions mentioned above.
class MeasurementCWT(nn.Module):
# CWT-based freq-time-dependent measurement
def __init__(self, npts, dt, fmin, fmax, amplitude_threshold=0.1, max_phase_diff=2.0*np.pi/3.0,
dj=1/12, s0=-1, J=-1, wavelet=None, fft_len=None):
super(MeasurementCWT, self).__init__()
if wavelet is None:
wavelet = Morlet(6)
# Smallest resolvable scale
if s0 == -1:
s0 = 2 * dt / wavelet.flambda()
# Number of scales
if J == -1:
J = int(np.round(np.log2(npts * dt / s0) / dj))
# The scales as of Mallat 1999
sj = s0 * 2 ** (np.arange(0, J + 1) * dj)
# Fourier equivalent frequencies
freqs = 1 / (wavelet.flambda() * sj)
if fft_len is None:
fft_len = int(2 ** np.ceil(np.log2(npts)))
self.fft_len = fft_len
ftfreqs = 2 * np.pi * np.fft.fftfreq(fft_len, dt)
sj_col = sj[:, np.newaxis]
psi_ft_bar = ((sj_col * ftfreqs[1] * fft_len) ** .5 *
np.conjugate(wavelet.psi_ft(sj_col * ftfreqs)))
self.psi_ft_bar = nn.Parameter(torch.from_numpy(psi_ft_bar), requires_grad=False)
self.freq_mask = nn.Parameter(torch.from_numpy(np.tile(np.logical_and(freqs <= fmax, freqs >= fmin), (fft_len, 1)).T), requires_grad=False)
self.amplitude_threshold = amplitude_threshold
self.max_phase_diff = max_phase_diff
self.dt = dt
def forward(self, syn, dat):
syn_ft = torch.fft.fft(syn, n=self.fft_len)
dat_ft = torch.fft.fft(dat, n=self.fft_len)
syn_cwt = torch.fft.ifft(syn_ft * self.psi_ft_bar, axis=-1)
dat_cwt = torch.fft.ifft(dat_ft * self.psi_ft_bar, axis=-1)
ind = torch.logical_and(self.freq_mask, torch.abs(syn_cwt).ge(self.amplitude_threshold * torch.max(torch.abs(syn_cwt))))
phase_shift = torch.angle(syn_cwt * dat_cwt.conj())
ind = torch.logical_and(ind, torch.cos(phase_shift).ge(np.cos(self.max_phase_diff)))
phase_shift_mask = torch.masked_select(phase_shift, ind)
return torch.sum(phase_shift_mask * phase_shift_mask) * 0.5 * self.dt
class MeasurementFT(nn.Module):
# Fourier-based frequency-dependent measurement
def __init__(self, npts, dt, fmin, fmax, amplitude_threshold=0.1, max_phase_diff=2.0*np.pi/3.0, fft_len=None):
super(MeasurementFT, self).__init__()
if fft_len is None:
fft_len = int(2 ** np.ceil(np.log2(npts)))
self.fft_len = fft_len
freqs = np.fft.fftfreq(fft_len, dt)
self.freq_mask = nn.Parameter(torch.from_numpy(np.logical_and(freqs <= fmax, freqs >= fmin)), requires_grad=False)
self.amplitude_threshold = amplitude_threshold
self.max_phase_diff = max_phase_diff
self.dt = dt
def forward(self, syn, dat):
syn_ft = torch.fft.fft(syn, n=self.fft_len)
dat_ft = torch.fft.fft(dat, n=self.fft_len)
ind = torch.logical_and(self.freq_mask, torch.abs(syn_ft).ge(self.amplitude_threshold * torch.max(torch.abs(syn_ft))))
phase_shift = torch.angle(syn_ft * dat_ft.conj())
ind = torch.logical_and(ind, torch.cos(phase_shift).ge(np.cos(self.max_phase_diff)))
phase_shift_mask = torch.masked_select(phase_shift, ind)
return torch.sum(phase_shift_mask * phase_shift_mask) * 0.5 * self.dt
Now I perform the experiment with a waveform that contains two dispersive modes. For simplicity, I just use Adam with a fixed learning rate of 0.01, and update 50 iterations.
nt = 1024
dt = 1.0 / 128
fmin = 1.0
fmax = 4.0
wave_gen = MultiModeWave(nt, dt)
syn_wave_par1 = nn.Parameter(torch.tensor([3.0, 0.5, 2.0, 0.5, 0.0]), requires_grad=True)
syn_wave_par2 = nn.Parameter(torch.tensor([5.0, 0.6, 2.0, 0.4, 0.1*np.pi]), requires_grad=True)
syn_amp1 = 1.0; syn_amp2 = 2.0
syn = syn_amp1 * wave_gen(syn_wave_par1) + syn_amp2 * wave_gen(syn_wave_par2)
dat_wave_par1 = nn.Parameter(torch.tensor([2.9, 0.6, 2.0, 0.4, 0.1*np.pi]), requires_grad=False)
dat_wave_par2 = nn.Parameter(torch.tensor([5.1, 0.5, 2.0, 0.5, -0.1*np.pi]), requires_grad=False)
dat_amp1 = 1.5; dat_amp2 = 1.5
dat = dat_amp1 * wave_gen(dat_wave_par1) + dat_amp2 * wave_gen(dat_wave_par2)
# uncomment to use CWT measurement
measurement = MeasurementCWT(nt, dt, fmin, fmax)
# uncomment to use FT measurement
#measurement = MeasurementFT(nt, dt, fmin, fmax)
# L-BFGS optimizer, will converge faster
#optimizer = torch.optim.LBFGS([syn_wave_par1, syn_wave_par2], line_search_fn='strong_wolfe', history_size=5, lr=0.0001)
# Adam optimimzer, reasonably good
optimizer = torch.optim.Adam([syn_wave_par1, syn_wave_par2], lr=0.01)
max_iter = 50
syn_save = []
misfit_save = []
save_every = 1
for iter in range(max_iter):
def closure():
optimizer.zero_grad()
syn = syn_amp1 * wave_gen(syn_wave_par1) + syn_amp2 * wave_gen(syn_wave_par2)
loss = measurement(syn, dat)
loss.backward()
return loss
syn = syn_amp1 * wave_gen(syn_wave_par1) + syn_amp2 * wave_gen(syn_wave_par2)
loss = measurement(syn, dat)
print(f"{iter}: {loss.item()}")
if (iter % save_every == 0):
syn_save.append(syn.clone().detach().numpy())
misfit_save.append(loss.item())
optimizer.step(closure)
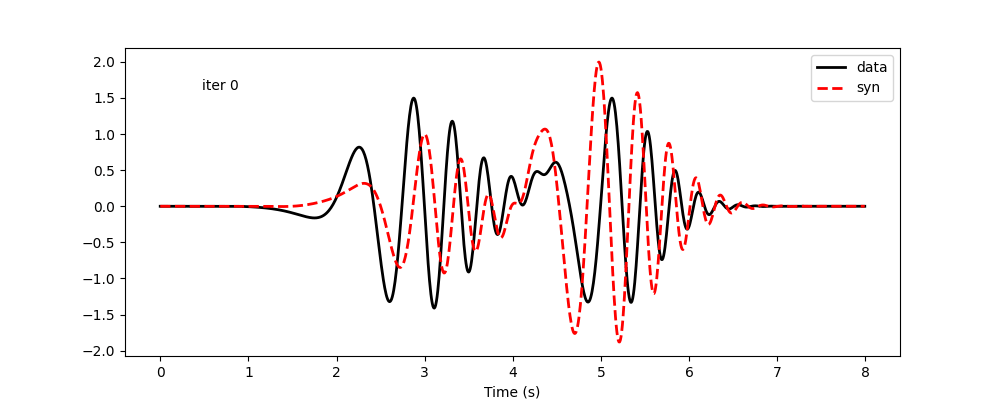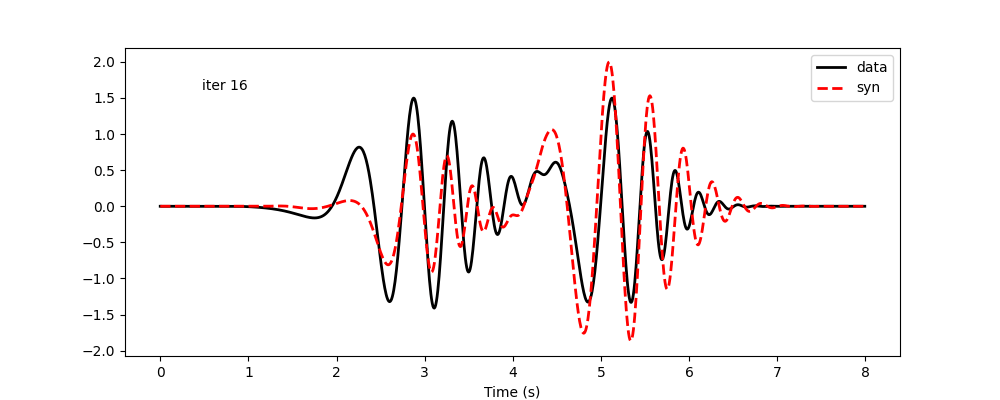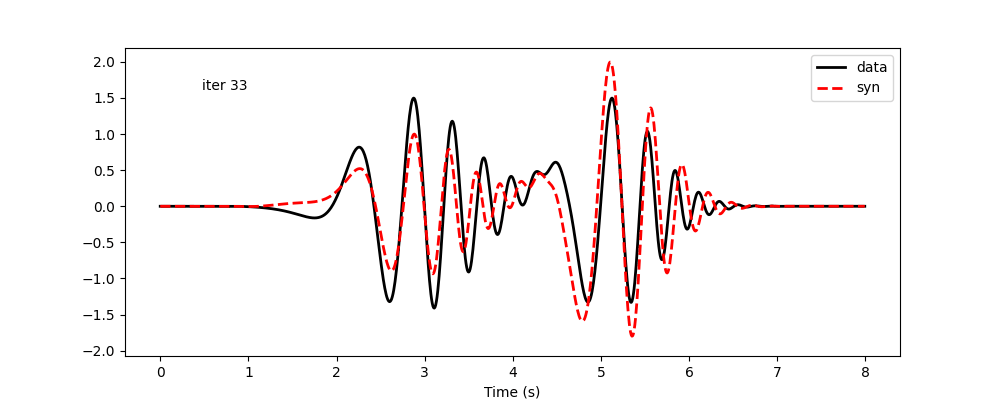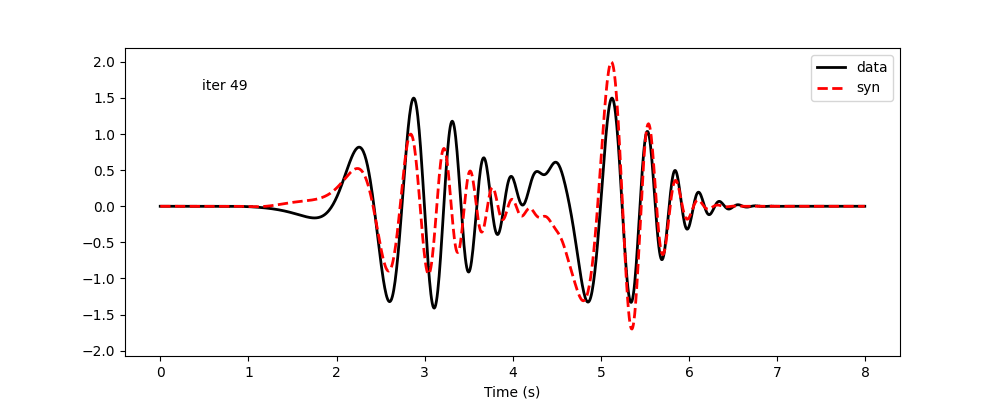
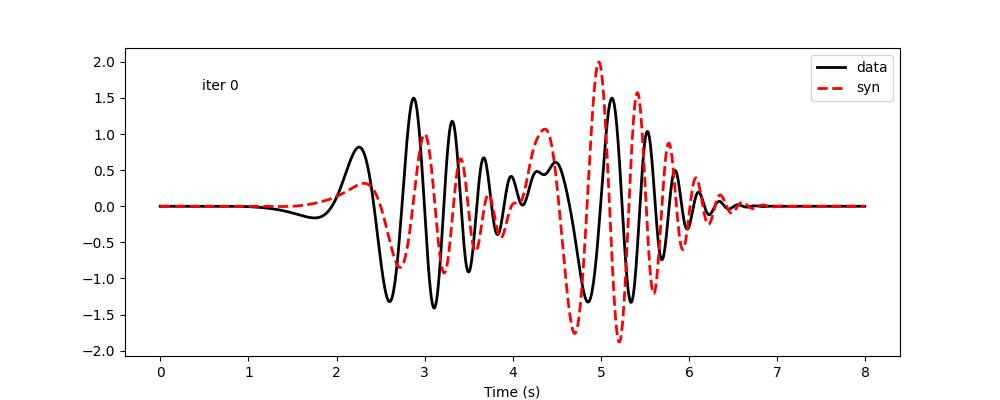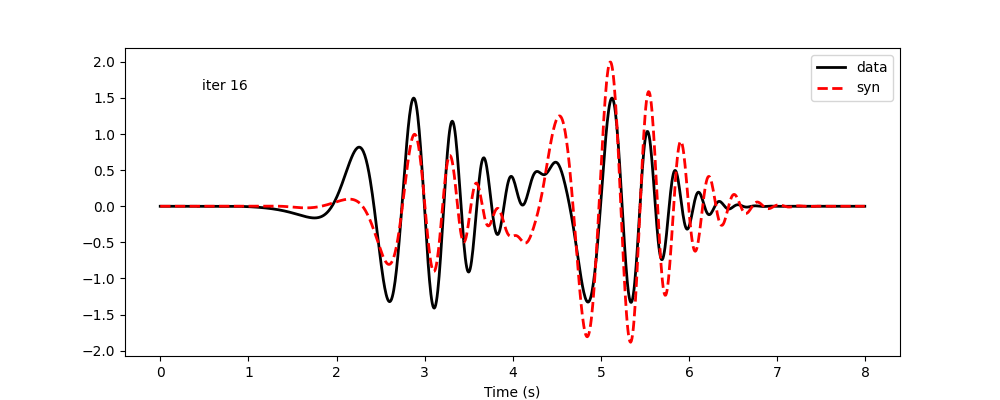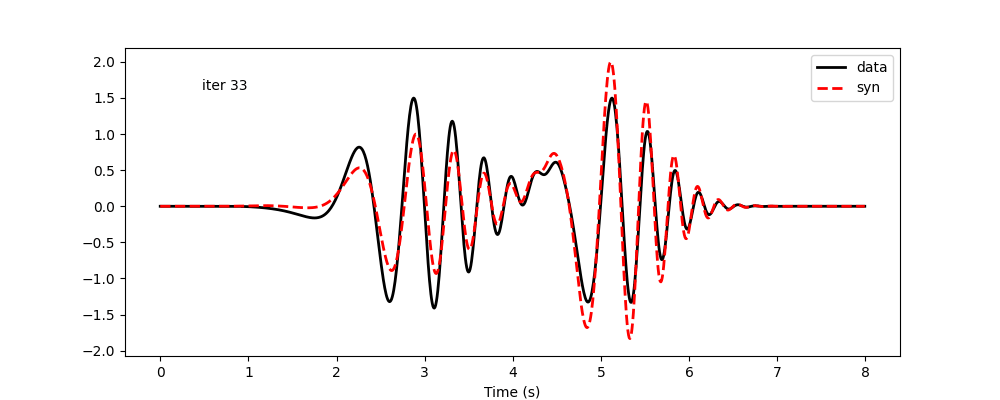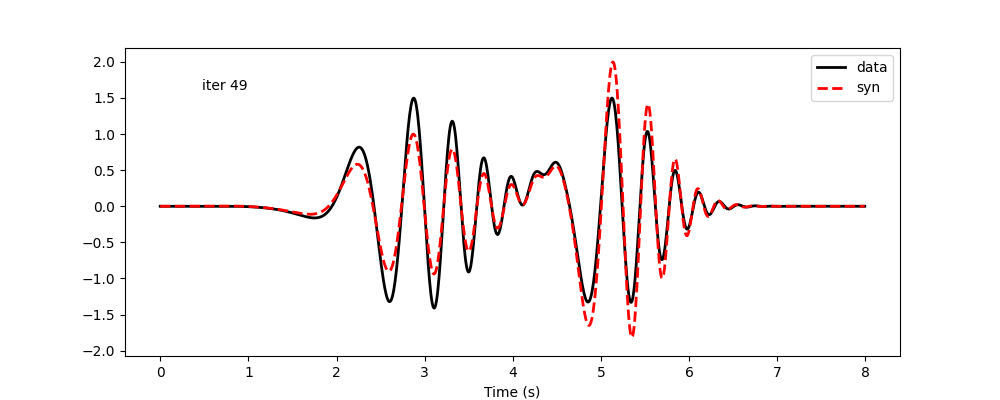
The code below is for visualization. The results follow. Again, amplitudes are considered not reliable and are not updated. Minimizing frequency-time-dependent phase shift allows both modes to be matched reasonably well. However, this is very hard using frequency-dependent phase shift, as it results in updates of global phase shifts, and the improvement in one mode will likely worsen the other.
t_arr = np.array(range(0, nt), dtype=float) * dt
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(t_arr, dat.clone().detach().numpy(), 'k', linewidth=2, label='data')
p = ax.plot(t_arr, syn_save[0], 'r--', linewidth=2, label='syn')[0]
txt = ax.text(0.1, 0.9, f'iteration 0',
horizontalalignment='left',
verticalalignment='top',
transform = ax.transAxes)
plt.legend()
plt.xlabel("Time (s)")
def animate(i):
p.set_ydata(syn_save[i])
txt.set_text(f"iter {i * save_every}")
anim = FuncAnimation(fig, animate, frames=len(syn_save))
# To save the animation using Pillow as a gif
writer = PillowWriter(fps=1,
metadata=dict(artist='Me'),
bitrate=300)
anim.save('measure_cwt.gif', writer=writer)
# Note: below is the part which makes it work on Colab
rc('animation', html='jshtml')
anim
Waveform update history using frequency-time-dependent phase-shift measurement:

Waveform update history using frequency-dependent phase-shift measurement: