We define and discuss the wavefield injection problem in the context of linear elasticity. The wavefield is governed by the elastic wave equation $$\rho\frac{\partial^2 \mathbf{u}}{\partial t^2}-\nabla\cdot(\mathbf{C}:\nabla\mathbf{u}) = \mathbf{f}\qquad \text{in}\ \oplus,$$ subject to certain boundary condition at $\partial\oplus$, where $\oplus$ denotes the entire medium of wave propagation (e.g., the whole Earth).
Now suppose that we have a local domain $\Omega\in\oplus$ in which structural perturbations exist and the wave propagations are of particular interest, but the source $\mathbf{f}$ is supported far away from $\Omega$, and directly solving the wavefield in $\oplus$ is too expensive. If we happen to have access to some background wavefield $\mathbf{u}^0$ outside $\Omega$ $$\rho^0\frac{\partial^2 \mathbf{u}^0}{\partial t^2}-\nabla\cdot(\mathbf{C}^0:\nabla\mathbf{u}) = \mathbf{f}\qquad \text{in}\ \oplus\setminus\Omega,$$ then it may be possible to reconstruct $\mathbf{u}$ using $\mathbf{u}^0$, with numerical simulations only performed in $\Omega$ (potentially in the neighbourhood of $\Omega$, but not in the entire $\oplus$).
As a more rigorous definition, if
If we define wavefield $$\mathbf{w}:=\left\{\begin{array}{ll} \mathbf{u} & \qquad \text{in}\ \Omega, \\ \mathbf{u}-\mathbf{u}^0 & \qquad \text{in}\ \oplus\setminus\Omega, \end{array}\right.$$ then $\mathbf{w}$ satisfies the source-free wave equation inside and outside $\Omega$ $$\rho\frac{\partial^2 \mathbf{w}}{\partial t^2}-\nabla\cdot(\mathbf{C}:\nabla\mathbf{w}) = 0\qquad \text{in}\ \oplus,$$ but $\mathbf{w}$ is discontinuous in its displacement and traction across the interface between $\Omega$ and $\oplus\setminus\Omega$: $$\mathbf{w}\Big|_{\Gamma+}^{\Gamma-} = \mathbf{u}^0\Big|_{\Gamma},$$ $$\hat{\mathbf{n}}\cdot(\mathbf{C}:\nabla\mathbf{w})\Big|_{\Gamma+}^{\Gamma-} = \hat{\mathbf{n}}\cdot(\mathbf{C}:\nabla\mathbf{u}^0)\Big|_{\Gamma}.$$
Solving the wave equation subject to prescribed displacement and traction discontinuity condition on an interface is called the interface discontinuity condition problem. It can be proven that the interface discontinuity condition problem is well-defined in the sense that the wavefield is uniquely determined by the interface discontinuity condition. It should be noted that in order to uniquely determine the solution, the displacement and traction discontinuities must be simultaneously provided. This is in contrast with the well-known boundary value problem, of which the solution can be uniquely determined by displacement or traction boundary condition.
Note that the kinematic fault simulation problem is a special case of the interface discontinuity condition problem: the displacement discontinuity is prescribed to be the slip on the fault, but the traction discontinuity must be zero because of Newton's third law. The full interface discontinuity condition problem of the elastic wave equation is rarely encountered in the real world, because there is hardly any case in which displacement and traction can jump across an interface. In comparison, the interface discontinuity condition problem for the Maxwell equation, which describes superficial charge and current, is more common.
By solving the interface discontinuity condition problem, we can simulate the injection of a background wavefield into a local domain containing scatterers.
This feature is supported in SPECFEM3D. Currently only CPU version is merged in the repository, GPU version will be merged soon.
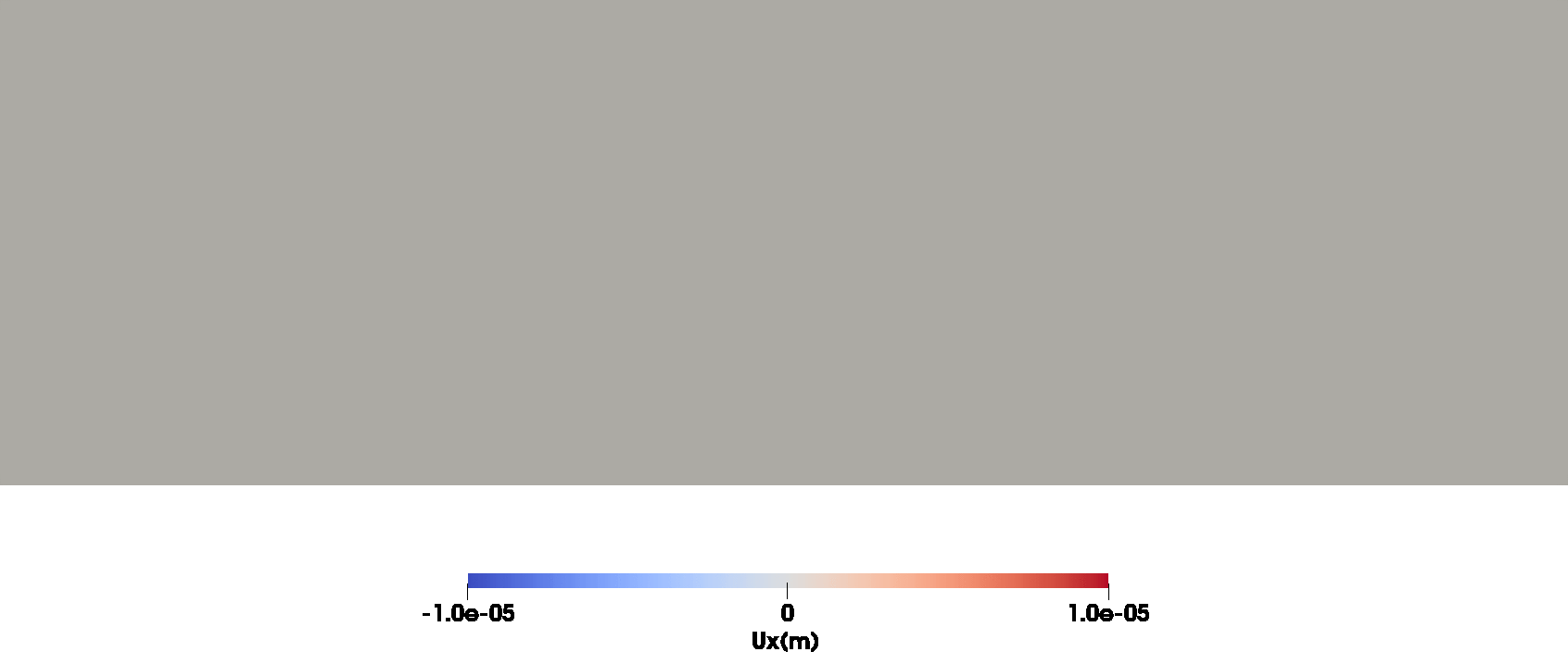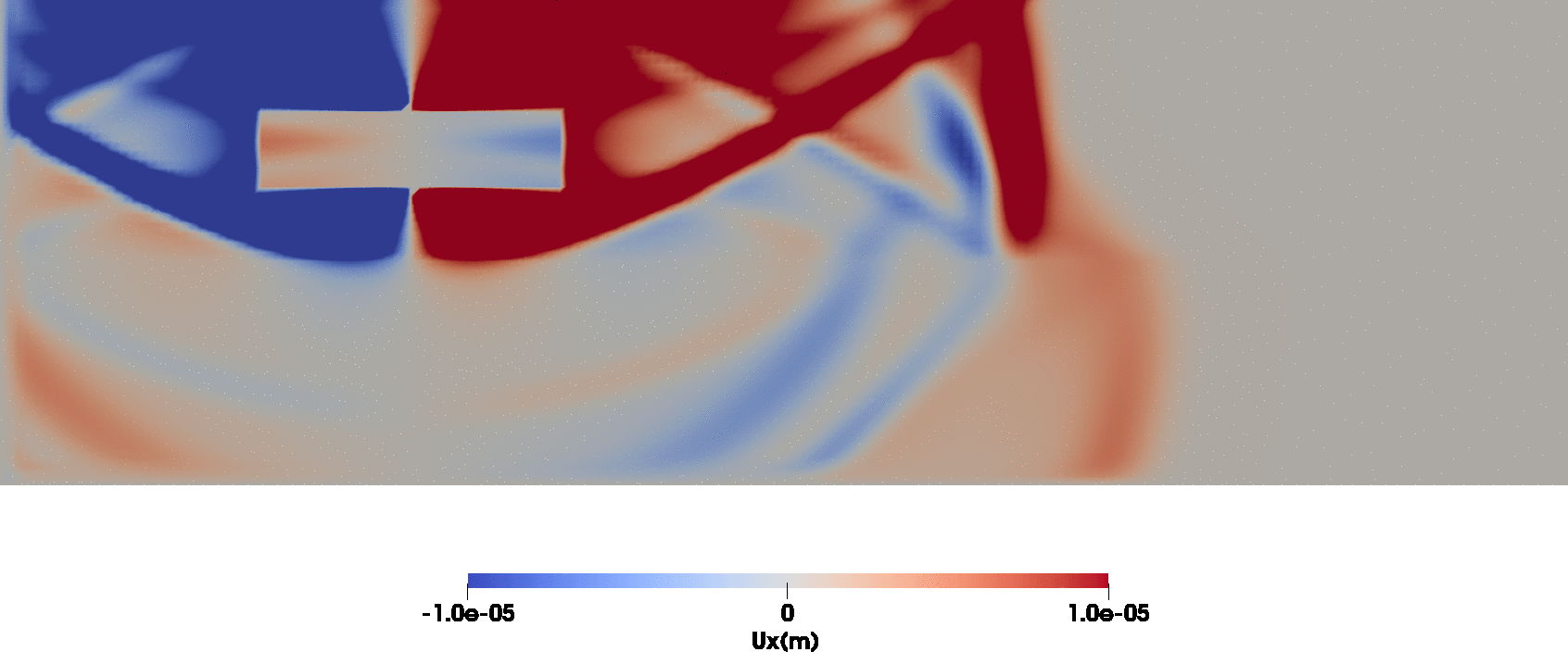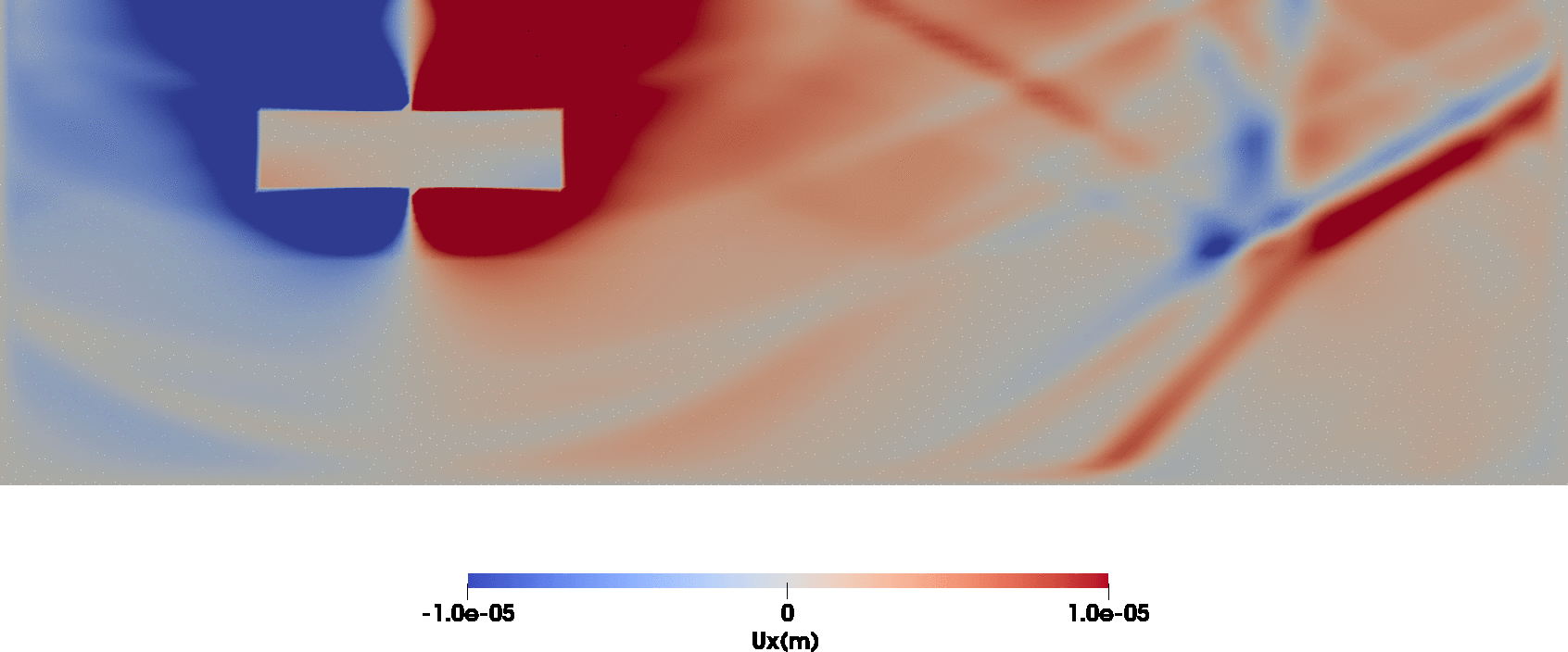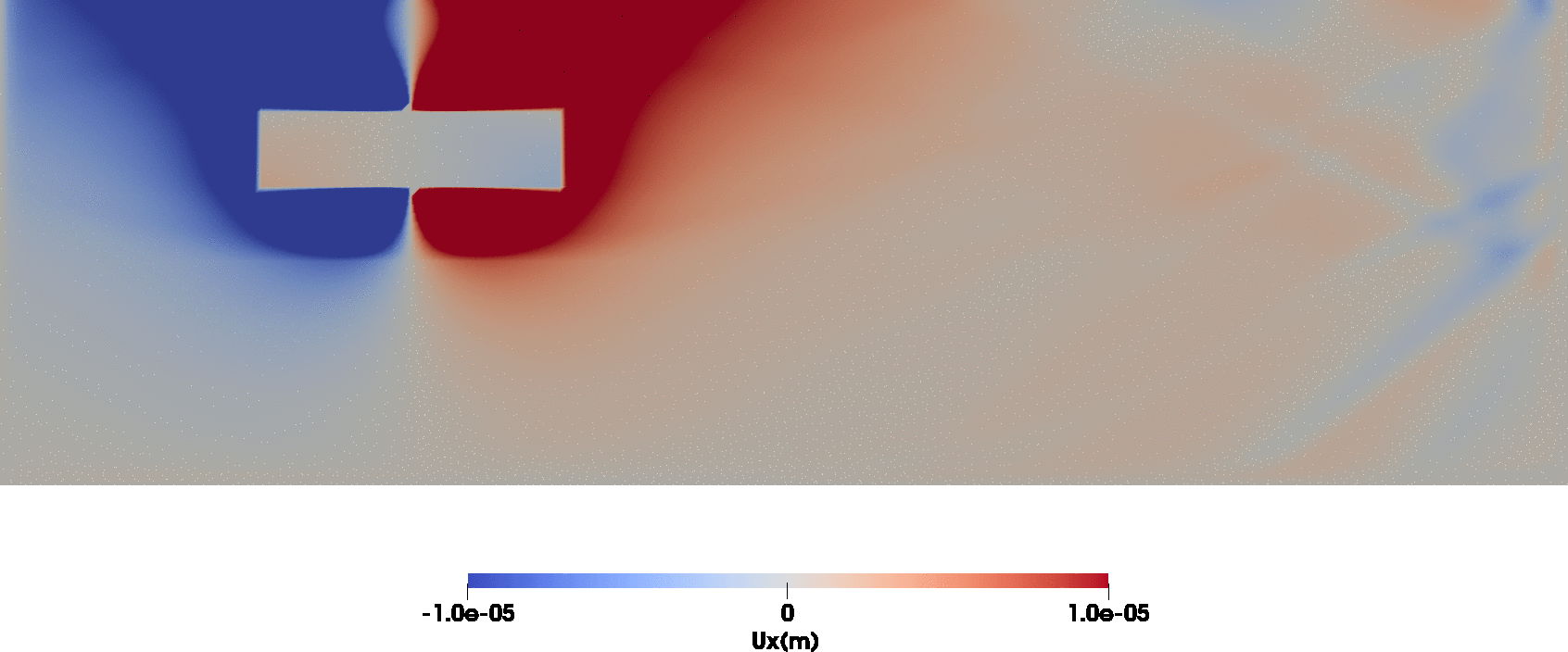
The animations below show the total wavefield $\mathbf{u}$ (left) and the solution to the interface discontinuity condition problem $\mathbf{w}$ (right).


Note that the wave can be injected from an inner domain into an outer domain (often referred to as wavefield extrapolation). The animation illustrates the injection of the wavefield excited by an explosion (Aki & Richards 2002, P77, eq. 4.29) into a layered half-space.